GeoGebra について お問い合わせ office@geogebraorg 利用規約 – プライバシー – ライセンス 言語 日本語 © 21 GeoGebra 2次関数の平行移動 作成者 嶋津恒彦 新しい教材 二次関数の平行移動 y = a x 2 y=ax^2 y = a x 2 を平行移動させたグラフで頂点が (p, q) (p,q) (p, q) となるものは, y − q = a (x − p) 2 yq=a(xp)^2 y − q = a (x − p) 2 となります。 x x x 軸方向に p p p , y y y 軸方向に q q q 平行移動です。 円の平行移動 中心 (a, b) (a,b) (a, b) ,半径 r r r の円の方程式は,MathAquarium例題2 次関数 2 2 平行移動・対称移動 (1) 2 次関数y=x2-2x+3 のグラフをx 軸方向に-1,y 軸方向に1 だけ平行移動したグラフの2 次関数 を求めよ。 (2) 放物線y=-3x2+2x+1 は,放物線y=-3x2-2x-1 をどのように平行移動すれば得られるか。 (3) 放物線y=x2-2x+3 を,次

2次関数のグラフの対称移動 Y Ax Bx Cのグラフをx軸 Y軸 原点に関して対称移動 数学i By ふぇるまー マナペディア
二次関数 平行移動 問題
二次関数 平行移動 問題- ・1次関数総まとめ問題(★★★☆☆)(21年度秋田県) 非常に無難な問題。 ・関数平行移動と無理やりな教育的・新共通テスト意識問題とgrapesの使い方(★★★☆☆)(21年宮城県) タイトルも長いが記事も長い。2次関数の定義 2次関数のグラフ y =x2 y = x 2 のグラフ , y =ax2 y = a x 2 のグラフ , y =a(x−p)2q y = a ( x − p) 2 q のグラフ , y= ax2bxc y = a x 2 b x c のグラフ ASCIIsvgによるグラフの描画 , 2次関数のグラフ(拡大,平行移動) 2次関数の平方完成の仕方 2次




二次関数 平行移動したものが2点を通る式を作る方法とは 数スタ
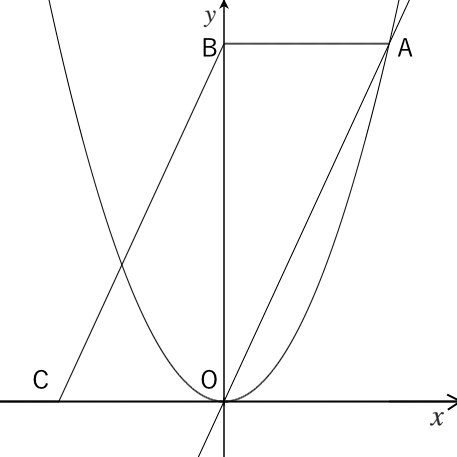
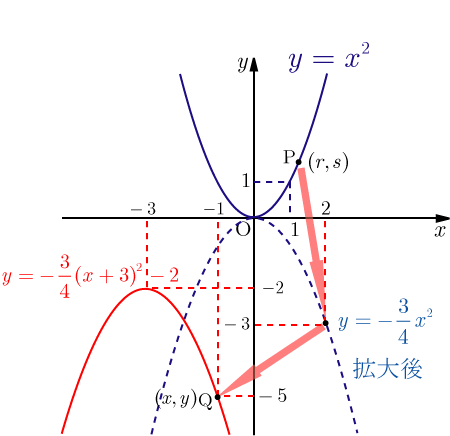
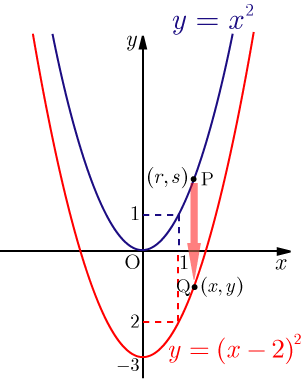
二次関数の作る図形に対し平行の等積変形を使って座標を求める問題です。 面積を求め、その面積に等しくなる放物線上の点を求める事もできます。 rはoをpqに平行な直線上を平行移動させた点、という条件がわかります。 二次関数のグラフと交点の7 3年2乗に比例する関数総合問題4 5問題 点a, p, qを頂点とする(誤)→点d, p, qを頂点とする(正) 3年2次方程式総合問題lv2 2(2)①と②の答が逆になっていたので訂正しました。 19/9/4 3年円周角6 ⑥答127°(誤)→ 117°(正) 例題 上で説明した内容を使って、問題を解いてみましょう。 標準放物線の平行移動(頂点に着目) で出てきた問題を解いてみます。 例題 放物線 y = 3x2 − 12x 10 y = 3 x 2 − 12 x 10 を x 軸方向に 1 1 、 y 軸方向に −2 − 2 だけ平行移動した放物線の方程式を求めなさい。 広告 解答 平行移動した後の放物線の方程式は y− (−2) = 3(x −1)2 − 12(x −1) 10 y −
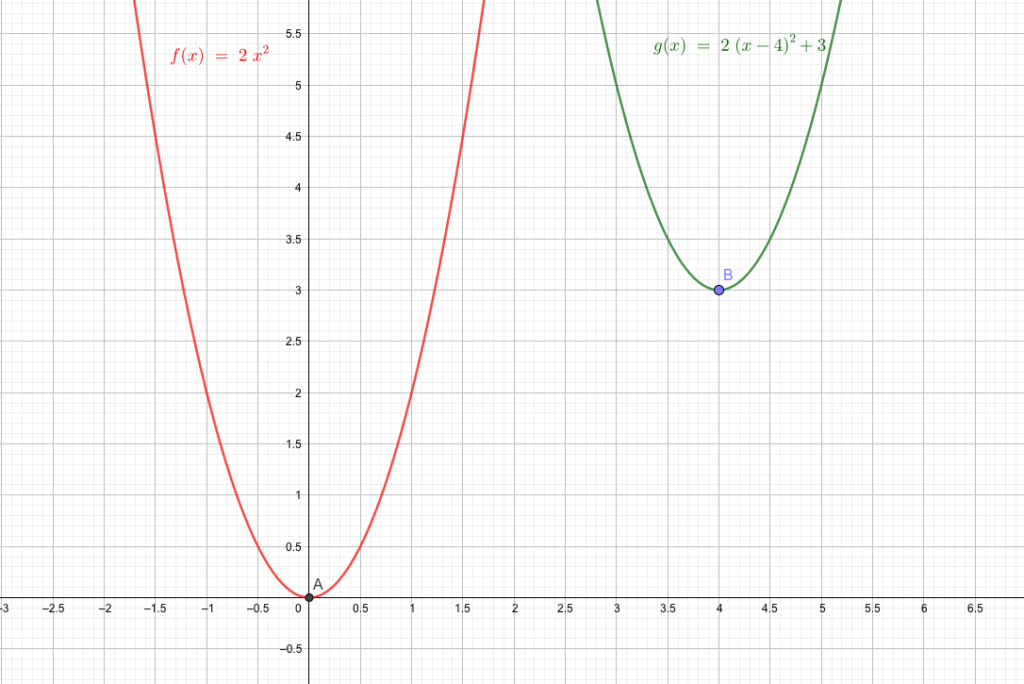
練習問題 次の二次関数を x 軸方向に3、y軸方向に2だけ平行移動させたものを求めよう。 y=x^ {2} y=2x^ {2} y=x^ {2}x1 y=x^ {2} の平行移動 y=x^ {2} を x 軸方向に3、y軸方向に2だけ平行移動させると、 \begin {eqnarray*} y&=& (x3)^ {2}2\\ &=& (x^ {2}6x9)2\\ &=&x^ {2}6x7 \end {eqnarray*} したがって求める二次関数は y=x^ {2}6x7問題B どれだけ平行移動すれば2つの放物線が重なるか(2次関数①は2次関数②をどのように平行移動したものか) 手順) ①移動する放物線の頂点A x y1 1, (スタート),移動先の放物線の頂点B x y2 2, (ゴール)を求める. 手順) ②頂点Aを平行移動して,頂点Bの位置に高校数学総覧 スポンサーリンク /5/13 数Ⅱ:式と証明の全面改訂を完了し、pdfの販売を開始。 /6/22 数Ⅱ:複素数と方程式の全面改訂を完了し、pdfの販売を開始。 /8/19 数Ⅱ:三角関数の全面改訂を完了し、pdfの販売を開始。 数B:ベクトル
二次関数の平行移動の解き方:公式はなぜマイナス? こにちは、今日は高校数学I、二次関数の平行移動のやり方について見てみましょう! 平行移動の公式、プラスとマイナスが混じって混乱しやすいですね。 もちろん、公式丸暗記でも問題ないこちらは、平行移動の公式、対称移動の公式にあてはめるだけなので、非常に簡単です。 aは二次関数の特長を利用しているのでこの単元でしか使えませんが、 bのやり方は、二次関数以外(三角関数、三次関数など)でも使う ことができます。 というか、bを使わないと解けません。 二次関数の問題です。分かりません、教えて下さい。 放物線y=2xの二乗4x+1・・・(1)がある。 放物線(1)をx軸方向にp、y軸方向にqだけ平行移動した放物線は 頂点のy座標が3で、点(3,5)を通る。 このとき定数p、qの値を求めよ。




高校数学 Y A X P 2のグラフ2 例題編 映像授業のtry It トライイット




高校数学 2次関数のグラフの平行移動の原理 受験の月
二次関数の平行移動・対称移動に関する問題は、 二次関数の頂点の移動に着目して ` y = a(xp)^2 q ` に代入して解く方法と、平行移動の公式、対称移動の公式に代入する方法があるよ。 公式を使った方が速いし、計算ミスも少なくなるので、ぜひ公式をマスターしよう。 平行移動・対称移動 数学Ⅰ 2次関数 平行移動・対称移動特訓① 問題編 数学Ⅰ 2次関数 平行移動・対称移動特訓① 解答編 最大・最小 <数字ver> 数学Ⅰ 2次関数 最大・最小特訓① <数字ver> 問題編 数学Ⅰ 2次関数 最大・最小特訓① <数字ver> 解答編 <定義域の右だけ動く> 0403二次関数の平行、対称移動(難易度2) 19/3/18 19/3/21 問題 関数を y 軸に対称移動し、 x 軸に 2 、y軸に − 1 平行移動すると、 y = − x 2 2 x 3 の関数となった。 元の関数を求めよ ヒント 対称移動と平行移動したときの、変数の置き換えを使います




高校数学の 二次関数の平行移動 に関する問題を解いてみる Yahoo 知恵袋より Makelemonadejp Com




教科書レベルの問題一覧と解答 数学 2次関数 教科書より詳しい高校数学
移動前の二次関数を求める問題 ある二次関数を 軸方向に 、 軸方向に だけ平行移動し、原点に関して対称移動したところ、 となった。 元の二次関数を求めなさい。 平行移動・対称移動から 二次関数の平行移動の問題です! 答えは2枚目です 解説の解き方がいまいちわかりません 他のやり方かこれのやり方を教えてください🙇♂️ 216 次の2次関数のグラフをx 軸万向に2, y軸方向に 3だけ平行移動した放物 線をグラフとする2次関数を求めよ2次関数の平行移動を使った問題 y=ax²のグラフを 平行移動 して、 ・ "y=a (xp)²" ・ "y=ax²+q" ・ "y=a (xp)²q" の形にすることはすでに学習済みかと思います。 ここでは、これらの平行移動のテクニックを使った練習問題を一緒に解いて、理解を深めていきましょう。




高校数学 放物線の平行移動1 重ねる 例題編 映像授業のtry It トライイット




二次関数の問題です 2 二次関数y Ax Bx Cのグラフをx軸方向に1 Y軸 高校 教えて Goo
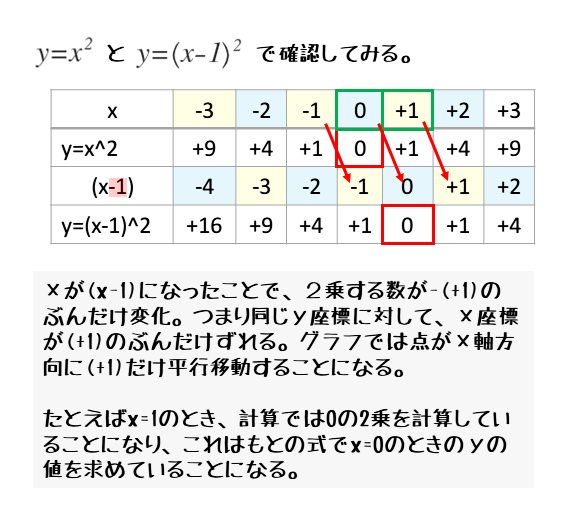
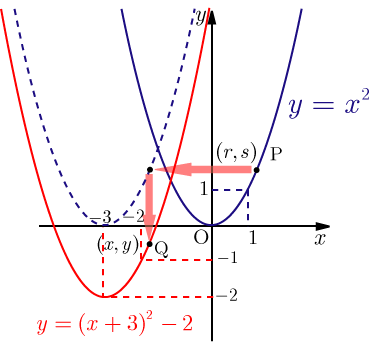
2次関数の移動に関するまとめ問題※例題1~8については 放物線の方程式を求めよ。 放物線 y = ax2 bx 8 を x 軸方向に 2, y 軸方向 c だけ平行移動して得られる放物線は y = x2 6x 15となるとき,a,b,c の値を求めよ。2次関数の平行移動 《解説》 2つの2次関数のグラフは, x 2の係数 a が一致すれば同じ形で,平行移動によって重なります. 移動の仕方は,頂点を比較すると分かります. 例1 2次関数 y= 2 x2 (A) のグラフの頂点の座標は (0,0) です.同様に,2次関数 y= 2 (x- 1) 2 + 5 高校数学の「二次関数の平行移動」に関する問題を解いてみる。 (Yahoo!知恵袋より) 18年10月15日 21年6月日 二次関数 実用数学技能検定(数学検定 数検), 数検準2級 読了時間 約 5 分 16 秒 問題 放物線 を平行移動したものが 2点 , を通るとき、その放物線の方程式を求めよ。




数学i 2次関数 2 6 放物線の平行移動 1 Youtube



3
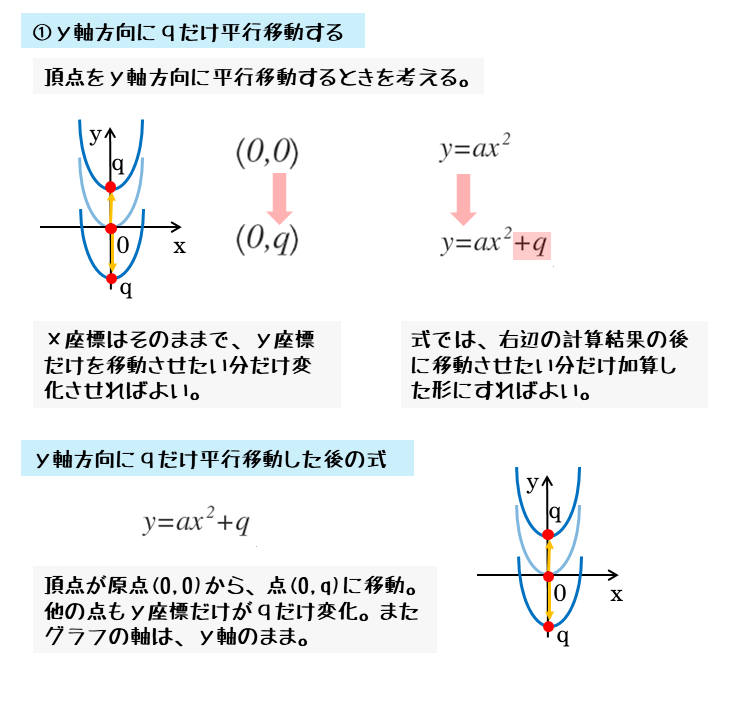
二次関数のグラフの平行移動と傾き 二次関数のグラフの平行移動は 傾き 、つまり x2 x 2 の係数が変化しない ということが大前提。 傾きが変化するとそれはもう平行移動じゃなくなるからね。 二次関数のグラフの平行移動 x x 軸方向に α α y y 軸方向に β β 平行移動 ・標準形 y=a(x−p)2q y = a ( x − p) 2 q を平行移動すると y=a(x−p−α)2 qβ y = a ( x − p − α) 2Q 関数\(y=x\sin x\)を\(x\)軸方向に3、\(y\)軸方向に1平行移動したグラフの方程式を求めよ。 A\(y1=(x3)\sin(x3)\) Q二次関数\(y=\left(x2\right)^24\)の頂点の座標を求めよ。 A\(y=x^2\)の頂点は\((0,0)\) \(y4=(x2)^2\)は\(y=x^2\)を 横に2;2次関数のグラフの平行移動 y=x²4x9 ここでは、この関数のグラフをx軸方向に4、y軸方向に−2平行移動したときに得られる放物線の方程式を求めてみましょう。 "y=ax²bxc"のグラフをx軸方向にp、y軸方向にq移動するというタイプの問題では、2通りの解き方があります。 ①グラフの頂点を求めて、頂点を平行移動して考える方法 ②"y=ax²bxc"のxをx−pに、yをyqに




高校数学 二次関数の平行移動 対称移動 Youtube




これで完璧 これであなたも二次関数が得意になる センター数学で必ず9割とらせます
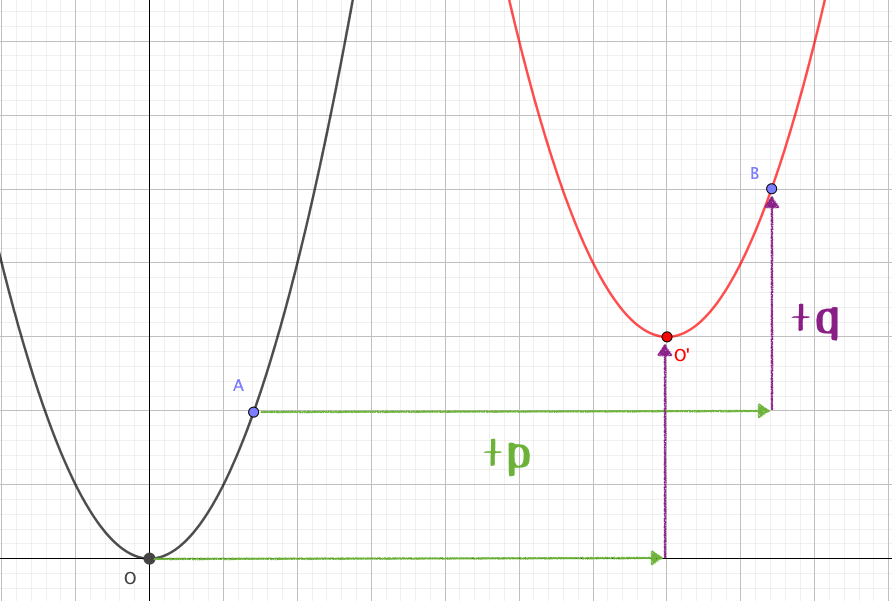
平行移動とは、「ある点を一定の方向に一定の距離だけ動かすこと」です。 高校数学では関数の平行移動というものを考えます。 関数は無数の点の集まりですから、この無数の点を一律に平行移動させると関数自体も平行移動することになります。 今回は、ある関数を平行移動させた結果、どのような関数になるかを求める方法の説明を行っていきます。 二次関数の平行移動は原点に戻した場合の関係性で考える y= (x2)^25 y = (x−2)2 5 のグラフを考えてみましょう。 ここで、教科書のおさらい。 q q 平行移動するとき、式は以下のように表すことができる。 5 5 を左辺に移項すると、このような式になり〔質問〕 y=x 2 +3x-3 を x軸方向に-3、y軸方向に2だけ移動させた放物線は、なぜ y+2=-2(x-3) 2 +5(x-3)+4 ではなく、y-2=-2(x+3) 2 +5(x+3)+4 という式で求めるのですか? 〔回答〕 まず、2次関数に限らず、実際の平行移動の問題を解くに当たっては、x軸方向に+p、y軸方向に+q 平行




2次関数のグラフの対称移動 Y Ax Bx Cのグラフをx軸 Y軸 原点に関して対称移動 数学i By ふぇるまー マナペディア




2次関数のグラフの対称移動 Y Ax Bx Cのグラフをx軸 Y軸 原点に関して対称移動 数学i By ふぇるまー マナペディア
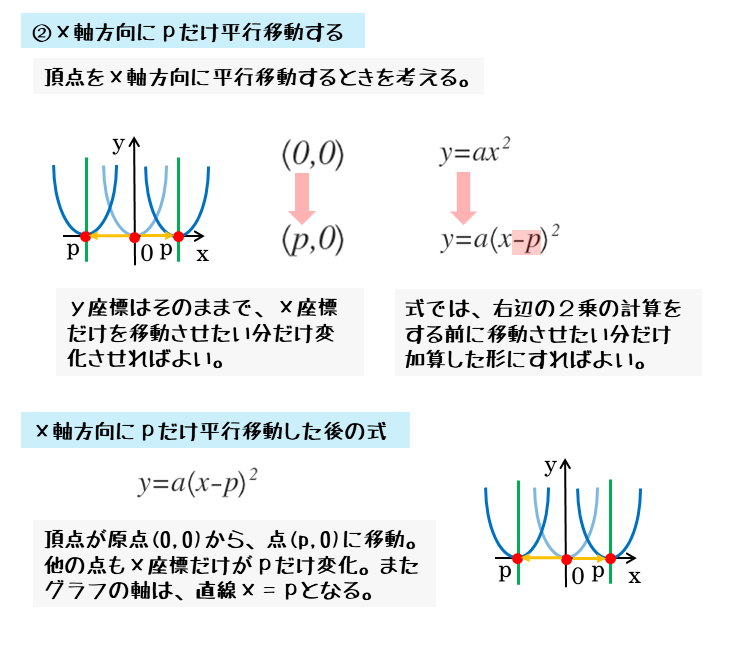
例題② を 軸方向に 、 軸方向に だけ平行移動したグラフの式を求めよ。 二次関数の場合も考え方はまったく同じで、元の関数の , を移動量に応じて置き換えます。 式の中に複数個所 があっても、それぞれを置き換えればOKです。 解答 を 軸方向に 、 軸方向に だけ平行移動すると、 答え: 最初の置き換えさえうまくいけば、あとは式をきれいに整えてあげる




2次関数12 平行移動対称移動のよくある誤謬 怜悧玲瓏 高校数学を天空から俯瞰する



2次関数 2次関数のグラフの平行移動について 日々是鍛錬 ひびこれたんれん



平行移動のやり方と公式の意味 符号を入れ替えて書き換えるだけで グラフの問題がスラスラ解ける 青春マスマティック




2 グラフの移動 Pukiwiki



2次関数の平行移動




二次関数 グラフの平行移動を具体例で詳細解説 式の仕組みから理解できます Rikeinvest




二次関数の平行移動の問題で疑問です 公式ではx軸方向に平行移動ならx Pですよね な Clear




高校数学の 二次関数のちょっと複雑な平行移動 に関する問題を解いてみる Yahoo 知恵袋より Makelemonadejp Com




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ



二次関数の利用 グラフ系の問題 苦手な数学を簡単に




二次関数の問題です なぜ 2だけ平行移動するときにy 2になるかが分かりません Clear




関数平行移動と無理やりな教育的 新共通テスト意識問題とgrapesの使い方 21年宮城県 高校入試 数学 良問 難問




高校数学 放物線の平行移動1 重ねる 練習編 映像授業のtry It トライイット




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ



2次関数 2次関数のグラフの平行移動について 日々是鍛錬 ひびこれたんれん




頂点の平行移動が公式だけすぐにわかる方法 看護受験の必須 数学の公式を確認テスト Vol23 Kazアカデミー 大阪の看護学校 看護予備校



48s96ub7b0z5f Net Nijikansu Taisyoido




公式 関数の平行移動について解説するよ 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ



高1の二次関数の平行移動の時 ある放物線をx軸方向に1 y Yahoo 知恵袋




平行移動のやり方と公式の意味 符号を入れ替えて書き換えるだけで グラフの問題がスラスラ解ける 青春マスマティック




高校数学 数 勉強動画 2次関数 移動編の問題 19ch



2次関数 2次関数のグラフの平行移動について 日々是鍛錬 ひびこれたんれん




3講 グラフの平行移動 2章 1節 2次関数とグラフ 問題集 高校数学



1



2次関数のグラフの拡大 平行移動に関する問題




二次関数 平行移動したものが2点を通る式を作る方法とは 数スタ



平行移動のやり方と公式の意味 符号を入れ替えて書き換えるだけで グラフの問題がスラスラ解ける 青春マスマティック




数 2次関数 関数の平行移動 操作は簡単 意味は深い 教えたい 人のための 数学講座



平行移動とは 1分でわかる意味と定義 やり方 二次関数との関係




平面座標上の関数の平行移動 身勝手な主張



必修 2 2 二次関数のグラフの平行移動 対称移動 わかりmath




数学 2次関数 平行移動 基本 オンライン無料塾 ターンナップ



2次関数のグラフの平行移動に関する問題




3分で誰でもわかる 平行移動の公式とやり方を見やすい図で解説します 高校生向け受験応援メディア 受験のミカタ



平行移動とは グラフ 二次関数など の平行移動の公式と作図 受験辞典




2次関数の平行移動の問題 高校数学ブログ
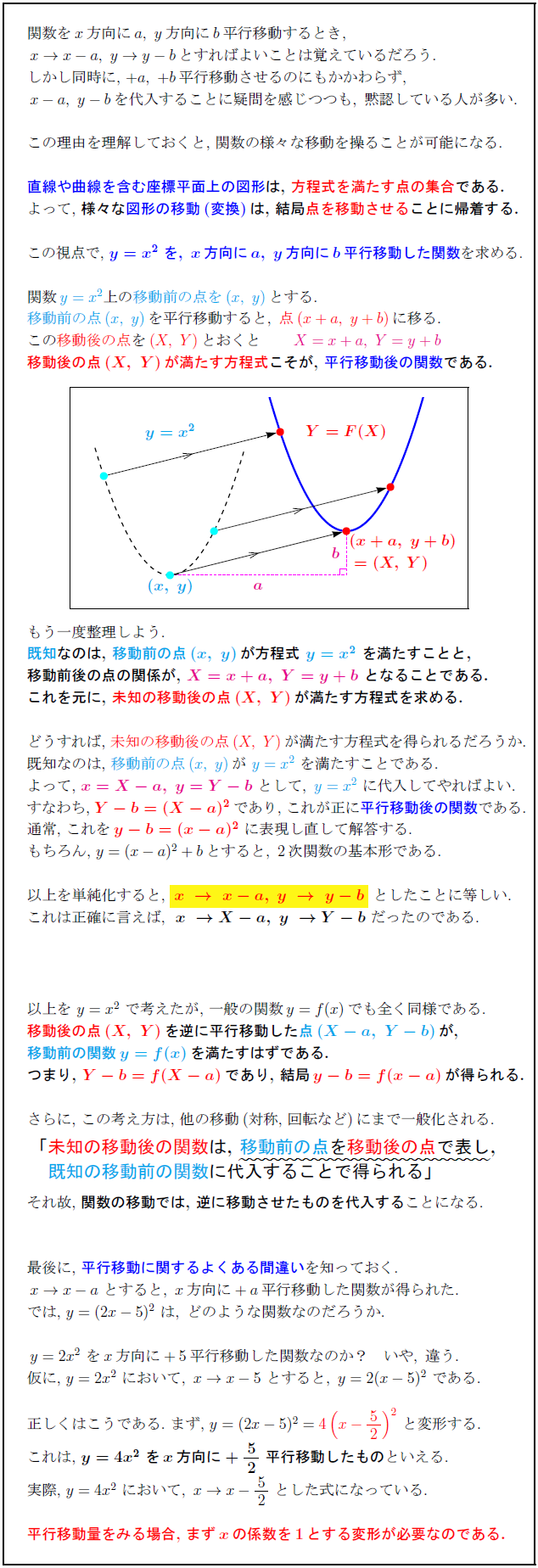



高校数学 平行移動の原理 X方向に A平行移動するのにx Aを代入する理由 受験の月
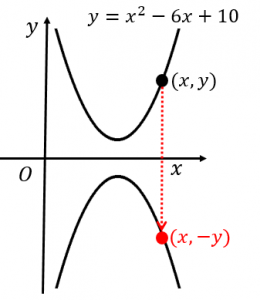



二次関数のx軸 Y軸 原点に関する対称移動 具体例で学ぶ数学




二次関数のグラフの平行移動とは 公式や応用問題3選をわかりやすく解説 遊ぶ数学
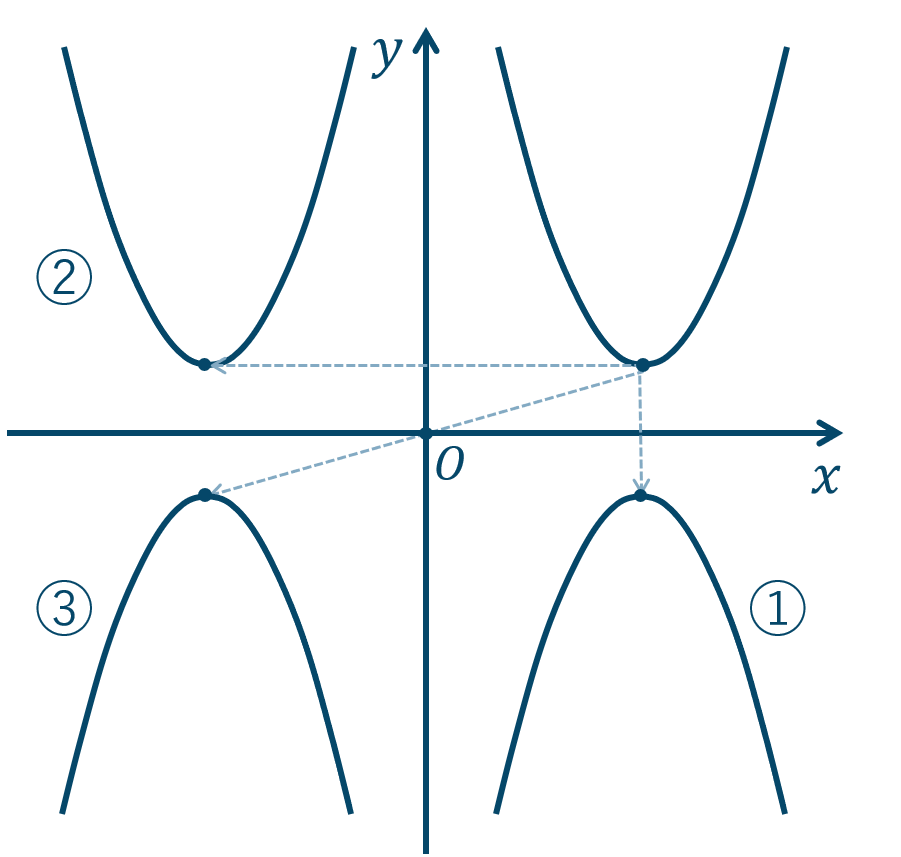



数学 グラフの対称移動のやり方とコツ ページ 2 教科書より詳しい高校数学
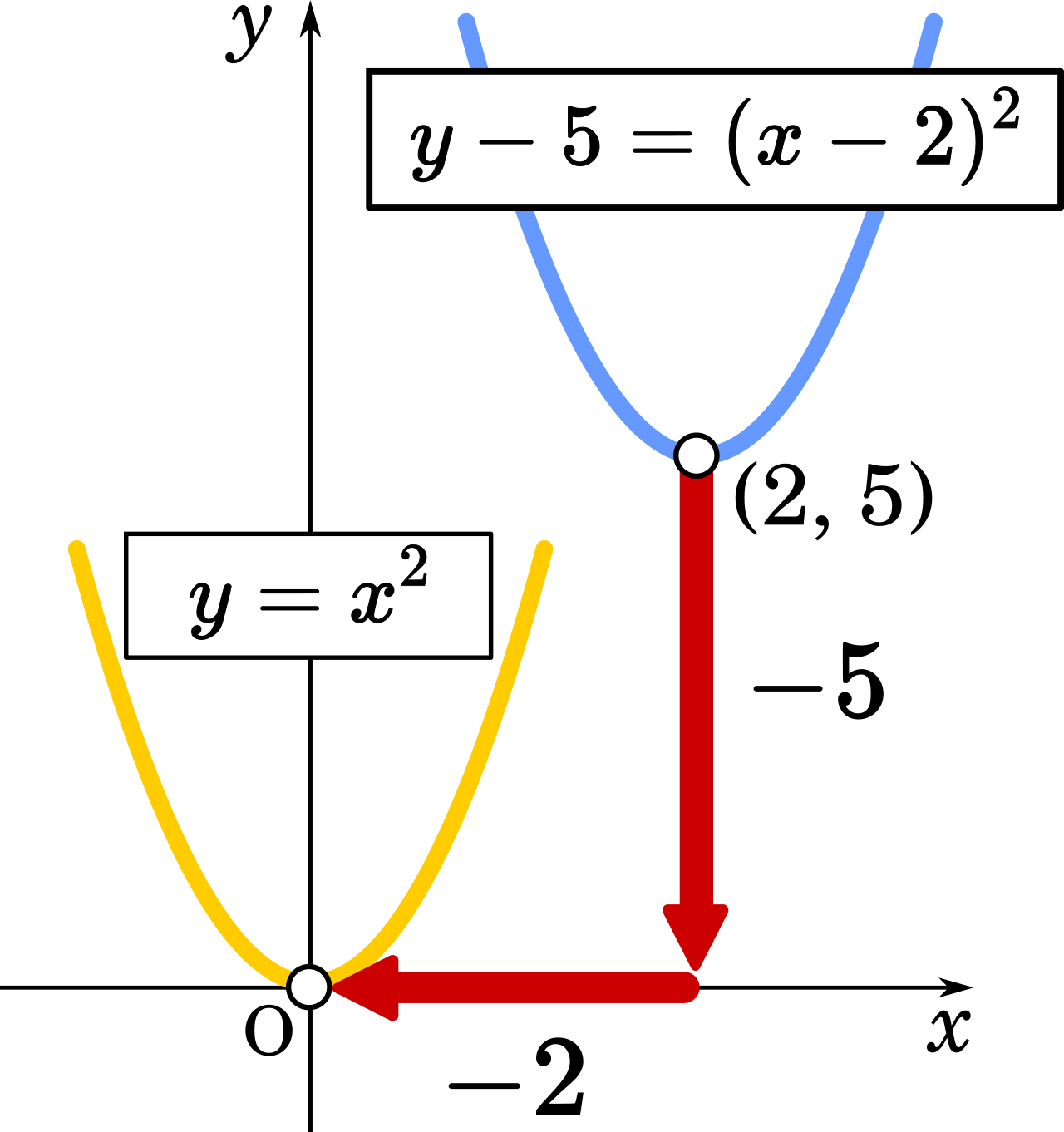



数 二次関数 平行移動の符号はなぜ反対になるのか 答えは見方が逆だから Mm参考書



平行移動とは グラフ 二次関数など の平行移動の公式と作図 受験辞典




2次関数の移動に関する問題まとめ チャート 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



二次関数の問題 平行移動によって重ねあわすことのできるものはどれ Yahoo 知恵袋




二次関数 グラフの平行移動を具体例で詳細解説 式の仕組みから理解できます Rikeinvest



1




3講 グラフの平行移動 2章 1節 2次関数とグラフ 問題集 高校数学




図解 グラフの平行移動がなぜマイナスで書かれるか本気で解説してみた 理系のひとりごと



48s96ub7b0z5f Net Nijikansu Taisyoido
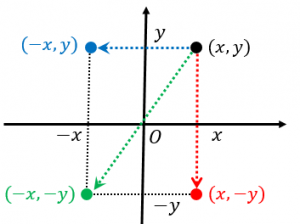



二次関数のx軸 Y軸 原点に関する対称移動 具体例で学ぶ数学




高校数学 2次関数のグラフの対称移動の原理 X軸 Y軸 原点 受験の月




発展 グラフの平行移動 なかけんの数学ノート




二次関数のグラフを平行移動させる公式と証明 なぜマイナスになるの
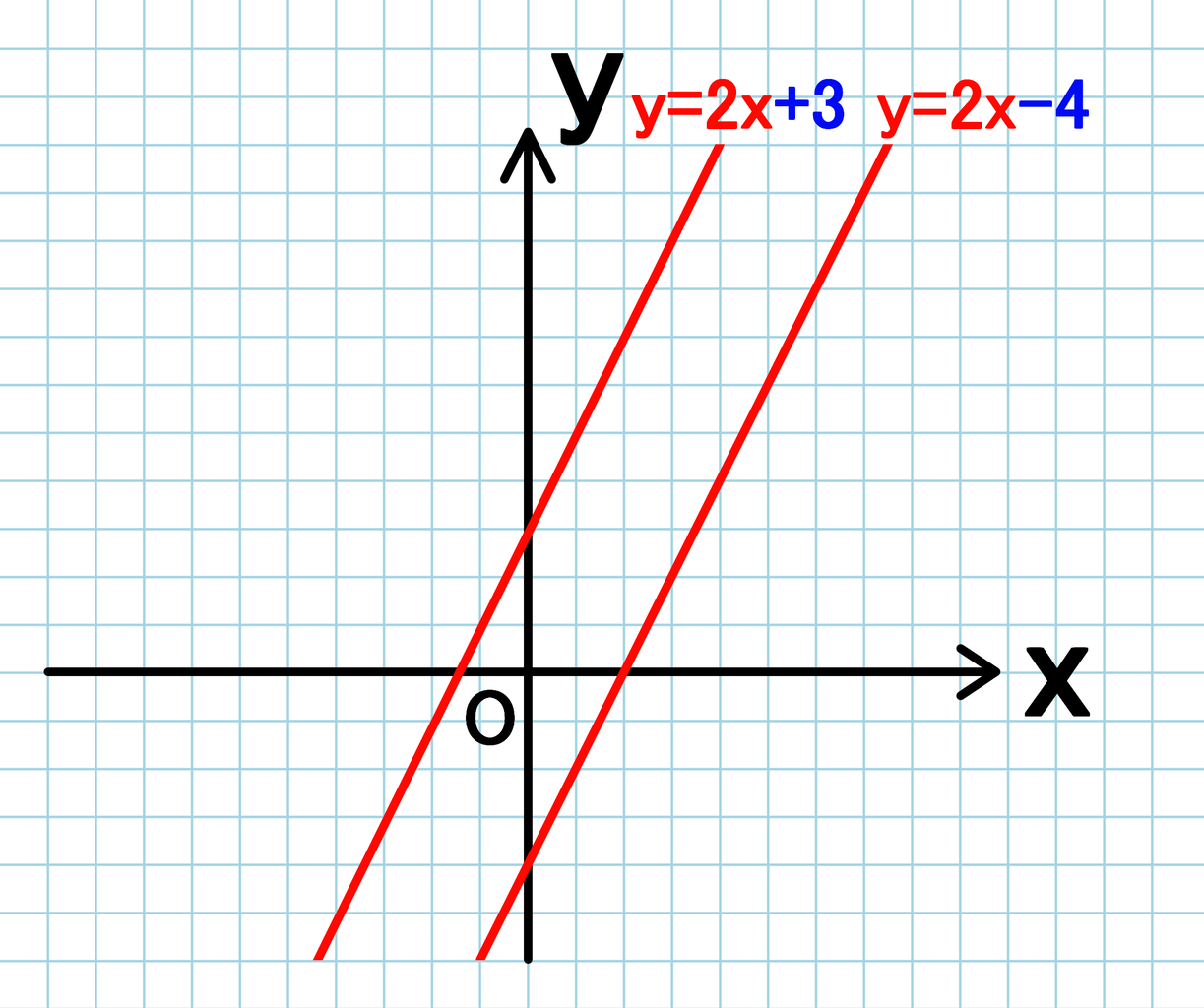



グラフ同士の関係 平行移動 直角に交わる 軸に対して対称 バカでもわかる 中学数学




二次関数 どのように平行移動したら重なる 例題を使って問題解説 数スタ



1




二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局




3分で誰でもわかる 平行移動の公式とやり方を見やすい図で解説します 高校生向け受験応援メディア 受験のミカタ
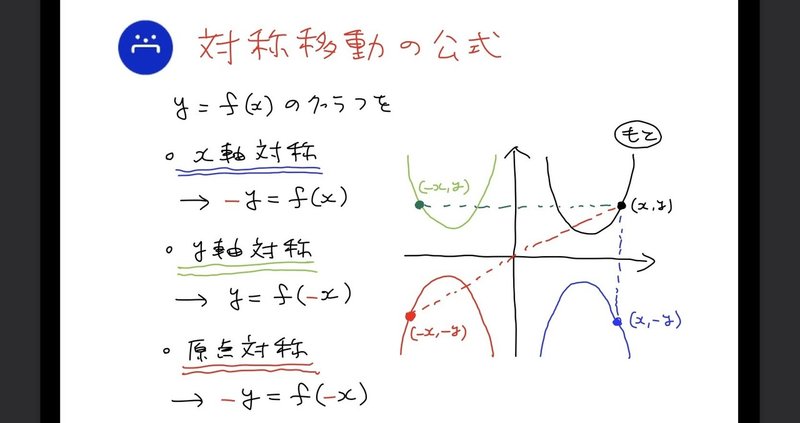



高校数学無料問題集 数 第2章 2次関数 平行移動と対称移動 桝 ます Note



数1の問題です 二次関数の平行移動の問題で 答えの数字自体はあっているのに Yahoo 知恵袋



二次関数の移動




3次関数の分類と点対称性 おいしい数学
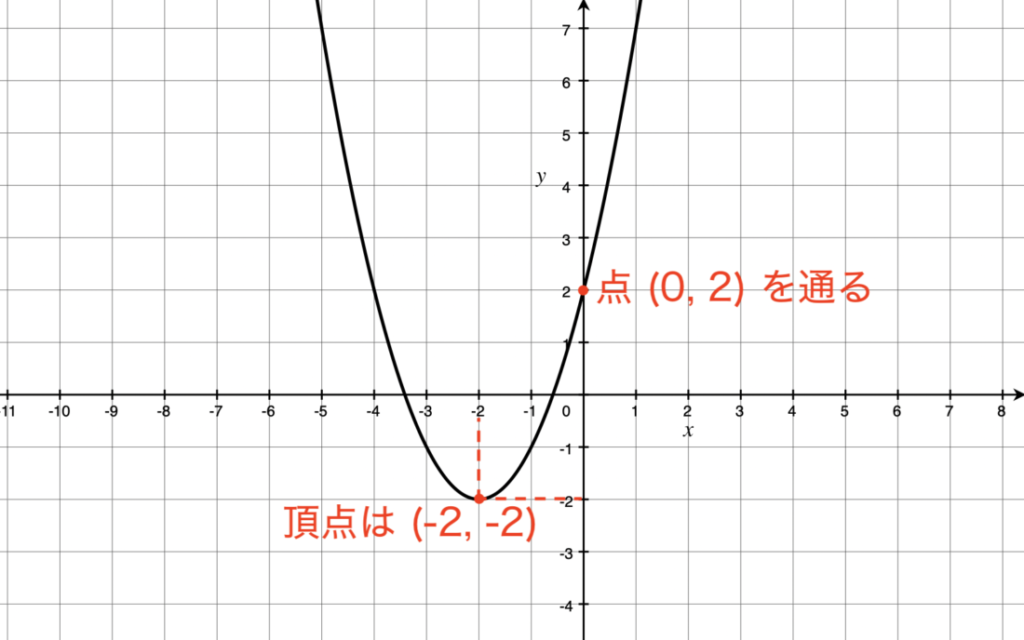



二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局



まとめ 2 2 二次関数のグラフの平行移動 対称移動 わかりmath




数 2次関数 関数の決定その1 頂点と軸が分かる場合 平行移動と媒介変数がポイント 教えたい 人のための 数学講座




2次関数の問題に対する条件反射 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



進むのにマイナスとは これ如何に 図形の平行移動 理系男子の独り善がり




二次関数のグラフの平行移動とは 公式や応用問題3選をわかりやすく解説 遊ぶ数学




高校数学 数 41 2次関数 移動編 Youtube




数学 2次関数の 対称移動 たいしょういどう ってどうやるの 高校数学 質問ありがとうございました 行間 ぎょうのあいだ 先生



二つの2次関数グラフの位置関係 平行移動 デジタル教科書 電子教科書



X軸方向に平行移動とは 1分でわかる意味 公式 Pとqの関係



48s96ub7b0z5f Net Nijikansu Heikoido



2次関数とは 1分でわかる意味 公式と計算 グラフ 平行移動との関係



二次関数の移動
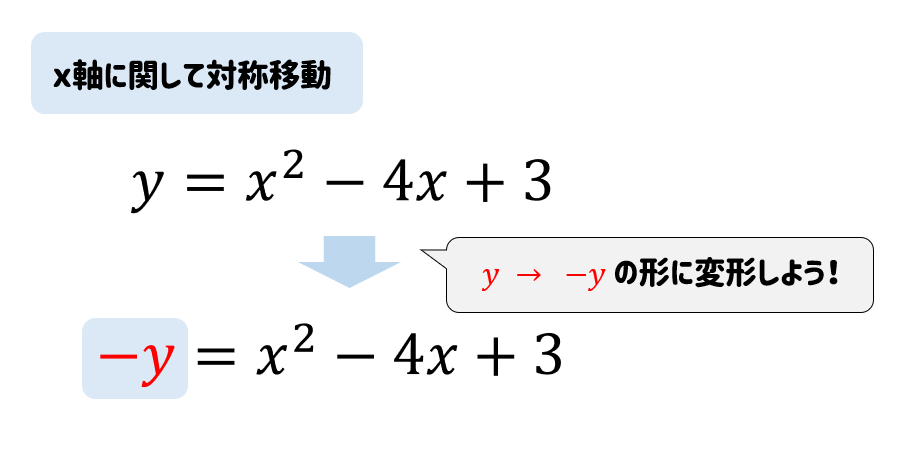



苦手な人向け 二次関数を対称移動したときの式の求め方を解説 数スタ




2次関数の対称移動 数学i フリー教材開発コミュニティ Ftext
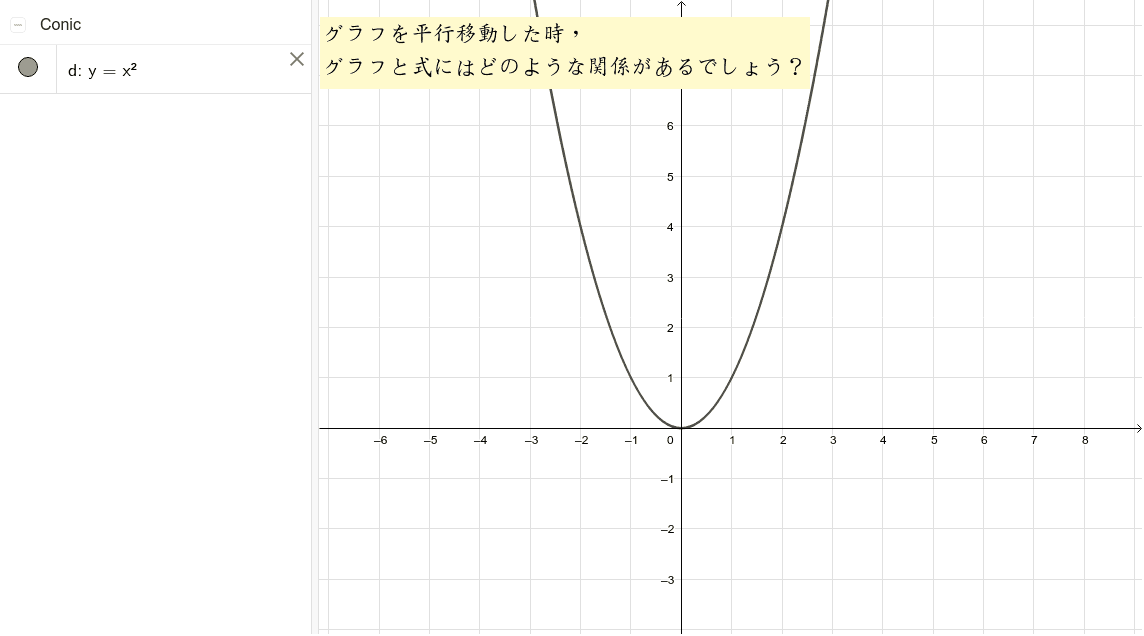



二次関数のグラフの平行移動 Geogebra



平行移動とは グラフ 二次関数など の平行移動の公式と作図 受験辞典




この問題がわかりません 教えてください おねがいします Clear
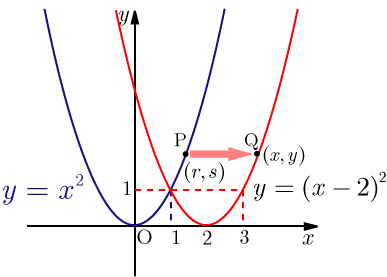



2次関数のグラフの平行移動に関する問題
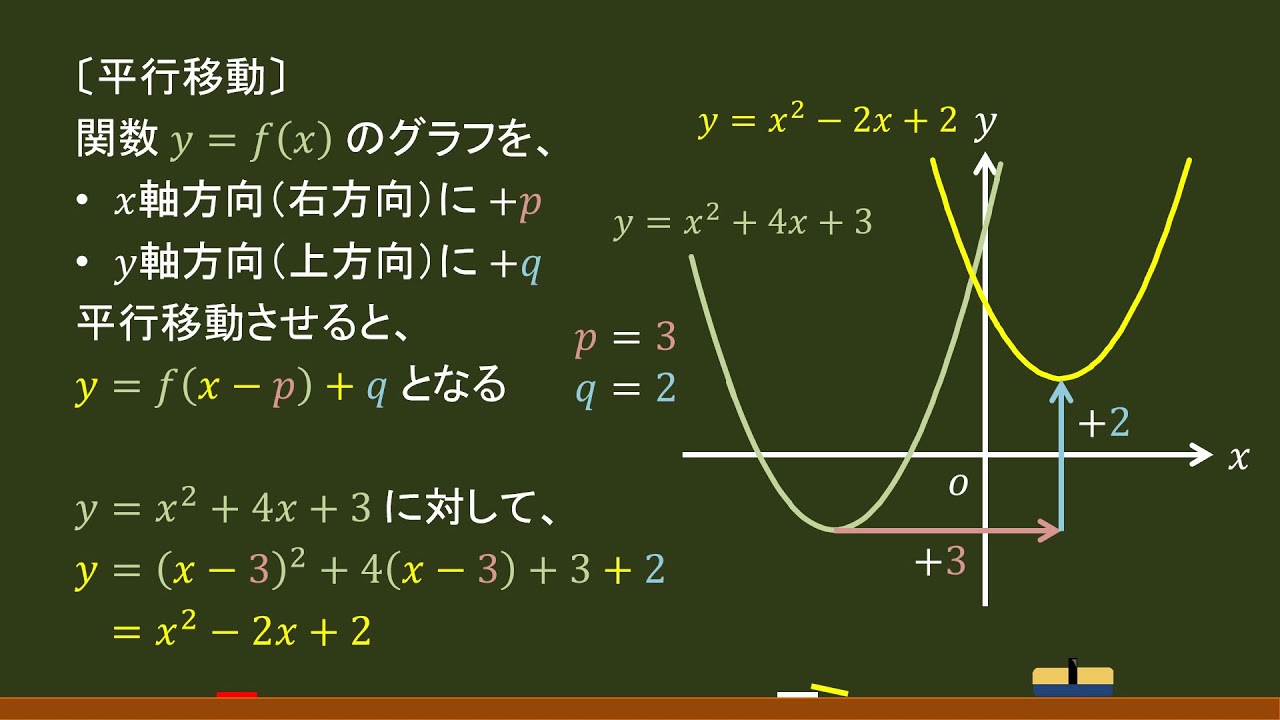



数学 2次関数 平行移動 基本 オンライン無料塾 ターンナップ




高校数学 2次関数の平行移動 2次関数の平行移動は2通りの方法をおさえること Clear




二次関数のグラフを平行移動させる公式と証明 なぜマイナスになるの




二次関数のグラフの平行移動とは 公式や応用問題3選をわかりやすく解説 遊ぶ数学



2次関数のグラフの平行移動に関する問題




標準 放物線の対称移動 なかけんの数学ノート




数 2次関数 対称移動 1つの知識から広く深まる世界 教えたい 人のための 数学講座




2次関数のグラフを 原点 X K Y Lに関して移動する方法 数学i By はっちゃん マナペディア




3分で誰でもわかる 平行移動の公式とやり方を見やすい図で解説します 高校生向け受験応援メディア 受験のミカタ




二次関数のグラフを平行移動させる公式と証明 なぜマイナスになるの



0 件のコメント:
コメントを投稿