ここからは、この平方根の小数部分についての計算式を、工夫して解く方法をご紹介します。 このように、3乗の式があるような複雑な問題の場合は、値を代入していって、徐々に係数を下げていく方法が有効な場合があります。 (星光学院高校) a a は22平方根 平方根の値を求めよう 4 3 年 組 氏名 1 の値を求めるのに,次のような2つの方法で解きました。 q にあてはまる数を求めよう。(近似値法) 60 2=,70=,802= だから, < < 次に,71 2=,72=, 732=,742== w 開平法(例)平方根(基礎) 素数と平方根(基礎) 平方根の計算(基礎) 平方根の計算2 平方根計算3 平方根計算4 平方根の大小など(基礎) 平方根問題7 平方根のおよその値 平方根計算5 平方根の大小 素因数分解

計算機プログラムの構造と解釈 第二版
7の平方根は
7の平方根は-25の平方根は,2乗したら25になる数なので, 5と-5となるね。 (2) ポイント 400の平方根の正の方を表しているので, はとなるね。 (3) ポイント は だから,7となるね。 2 , ,0 , ,2 , ポイント 正の数 a,b について, 平方根 次の問いに答えよ。 x 1 x = 7 のときx 4 1 x 4 の値を求めよ。 23 x=2− 2 のとき次の式の値を求めよ。 x 1 x 6− 2 2 x 3 1 x 3 90−49 2 4 x= 5 −2, y= 5 2のとき x 3 y−2x 2 y 2 xy 3 の値を求めよ。 16 次の問いに答えよ。 32 7 の整数部分と小数部分を求めよ




平方根 2乗するとaになる数 教遊者
7の平方根とは自乗(同じ数を2回かけること)して7になるような数です。 これを√7と書きます。 √7≒・・・・ ですが、これが無理数であることが知られています。平方根口诀表 👮👯👮💩👧👻👻👶 4,9,16不需要记住。 如果需要的话,记住2,3,5,7,11,13,17,19这几个值的平方根。 其他的:6=2*3,8=4*2,10=2*5,12=4*3,14=2*7,15=3*5,18=9*2,通过计算获得。 比如18的平方根就等于9的平方根乘以2的平方根=3*1414=4243 另外,有个开平与"7的平方根为(),的平方根是()."相关的知识点试题 (更多试题练习 中学题库 ) a、b为实数,在数轴上的位置如图所示,则的值是()。 下列说法正确的是 是81的一个平方根B数轴上的点与无理数 如图:数m在数轴上对应的点是A点,化简:﹣2m﹣2=_________. 如果x2=2,那么(x2)2等于( )A.16B.8C.4D.2 下列各式中正确的是 A.=±2B.=7C.=﹣D.=1
同類項は,次のようにまとめる ことができる。 ax+bx=(a+b)x 同類項 素因数分解 ある自然数を素因数だけの積 の形に表すこと 60=2²×3×5 3つの数の大小関係は,不等号 を使って,小さい順(あるいは, 大きい順)に並べて表す。 2<5<10 答 <1⑴ 10<42 ⑵ 52<30<62x2⑴ 5-2y ⑵ -x+3y 3⑴ 48=24×3 ⑵ 150=2×3×52 1年では数を2乗すること,2年では多平方根とは 2乗したらその数になるということです √7 × √7 =7 と(√7)×(√7)=7 が満たすので 答えは ±√7 となります (^^) 「平方数の数字根は 1, 4, 7, 9 の四通りの値しか取らない」ことの証明は 以下のような感じになると思い ます 。 証明 の前に、先に 数字 根の 重要 な 性質 について述べておき ます 。
数学 とその応用では、 二乗平均平方根 ( RMS または rms )は、 平均平方根 の 平方根 ( の 算術平均 )として定義されます。数値の セット の平方 )。 RMSは、 二次平均 とも呼ばれ、指数2の 一般化平均 の特定のケースです。RMSは、連続的に変化する 関数 に対しても定義できます。 7的算术平方根是√7 √7= √7≈ (精确到小数点后4位) 7は√49の平方根ということでしょうか? → √49は平方根ですが、7は平方根ではないです、値が同じだけです。 何でもかんでも√49=7 → 中学では教えているのかどうか私には判らないですが 2乗して7になる平方根は ±√49 と二つあります。




平方根 2乗するとaになる数 教遊者




中学数学 平方根 のコツ 平方根とは 平方根の大小
平方根 へいほうこん square root 実数 a に対して,x 2 =a を満たす実数 x を a の平方根と呼ぶ。 a が正数のとき a の平方根は正数であるものと負数であるものの二つが存在し,このうち正の方を√a で表す。 0の平方根は 0である。たとえば,√2=,√3=であり,これらは平方根(基礎) 素数と平方根(基礎) 平方根の計算(基礎) 平方根の計算2 平方根計算3 平方根計算4 平方根の大小など(基礎) 平方根問題7 平方根のおよその値 平方根計算5 平方根の大小 素因数分解平方根・累乗根 平方根・累乗根(グラフ) べき乗・累乗 階乗 階乗(グラフ)



0 64の平方根の値を求めるという問題なのですが なぜ平方根で Yahoo 知恵袋




根号 の意味と覚え方 ルートは 何のために作られた 三重の個人契約家庭教師
B >= 0 とする。このとき a < b p a < p b という定理を紹介しました。そこでは,この定理が正しいことを,図形を用いて 感じとってもらいました。 平方根を利用した図形問題は様々にあります。 例えば、このような問題は平方根の記号に関する基本的な理解をつかわなければなりません。 一辺がxの正方形の面積が10のとき、xを求めよ。 このような問題の場合 2乗して10になる自然数は何ですか?25の平方根は5と−5 の2つですが,そのうちの正の方を で表します. だから, です. 正の数 a に対して, a の平方根のうちで負の数の方を で表し,マイナス・ルート a といいます.これは, の符号だけを変えたものです. 例7 の2つですが,そのうちの




中学3年生 数学 平方根 問題プリント 無料ダウンロード 印刷 このページの答えのプリント 全部




ルート2 ルート3 ルート5の覚え方など 高校数学の美しい物語
平方根とは (ルートとは)|計算方法と求め方、語呂合わせと覚え方! 平方根とは × = × = の式が成り立つとき、 は の平方根と言います。 例えば、 2 ×2 = 4 2 × 2 = 4 なので、 2 2 は 4 4 の平方根と言います。 また、 −2 − 2 も2回かけると 4 4 になるので 回答 ベストアンサー 桃夏 1年以上前 7の平方根を根号を使って表す +√7と-√7 7を根号を使って表す √49 -7を根号を使って表す -√49 ややこしいけど、言葉の使い方で答えはちがってきます。 K🌿 1年以上前の2つだ。 これで平方根の求め方もマスターだ!^^ まとめ:平方根の求め方は√と±つければとりえあずok 平方根の求め方はむちゃくちゃ簡単。 ルートをかぶせて、±を左にくっつける。 最後にルートをはずせるかトライするだけ。




中学数学3年 平方根とその近似値 大小 有理数と無理数 受験の月




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ
平方根过程2 每一个过渡数都是由上一个过渡数变化而后,上一个过渡数的个位数乘以,如果需要进位,则往前面进1,然后个位升十位。 以此类推,而个位上补上新的运算数字。 简单地讲,过渡数27,是第一次商的1乘以,把个位上的0用第二次商的7来换,过渡数343是前两次商的17乘以=340,其中个位0用第三次商的3来换,第三个过渡数3462是前三次商173乘以=3460,把解答① 平方根 2② 2 ③ − (②と③は順不同) ④ 0 解説 例えば,2 乗して 25になる数が25の平方根なので,5だけ でなく−5もはいる。0 の平方根は0 だけであるが,それ以外 の場合は±の2 通りがある。また7 の平方根のように,整数・ 分数・小数で表すことができないものは,± 7 (プラス根号49=7,所以就变成了7的平方的平方根,7的平方=49,所以有变成49的平方根,所以就变成了7和7了 根号16为4,所以成了4的平方根,就是正负2 就是把正的和负的都写上,并且先算前面的,一步一步来 1年前 1 游佐银 幼苗 共回答了15个问题 向TA提问 举报 那是答案错了




3の平方根 Wikipedia




Dr 解析 構造力学事始め にご参加ください Drkouzoukaiseki Twitter
这是一个关于《平方根》实数PPT课件7,主要介绍了算术平方根的完整定义:正数a的正的平方根叫做a的算术平方根,0的平方根也叫做0的算术平方根等等内容。欢迎点击下载哦! 回顾 & 思考 1、我们已经学习过哪些运算?它们中互为逆运算的是?補講7 平方根の大小 70 はじめに 67 ページで, 定理(平方根の大小) a >= 0; この問題だと、√3=1732(与えられている条件)が使えるように、√300(数字)の形を変えよう! ということです。 もっと詳しく言うと、300 = 3×100 の100を、ルートの外に出して考えてみましょう。 √300 = 10√3 = 10×1732 = 1732 条件をもとに平方根の近似値を求める場合は その条件が使える形に、 数字の形を変える



1136 チャート事典
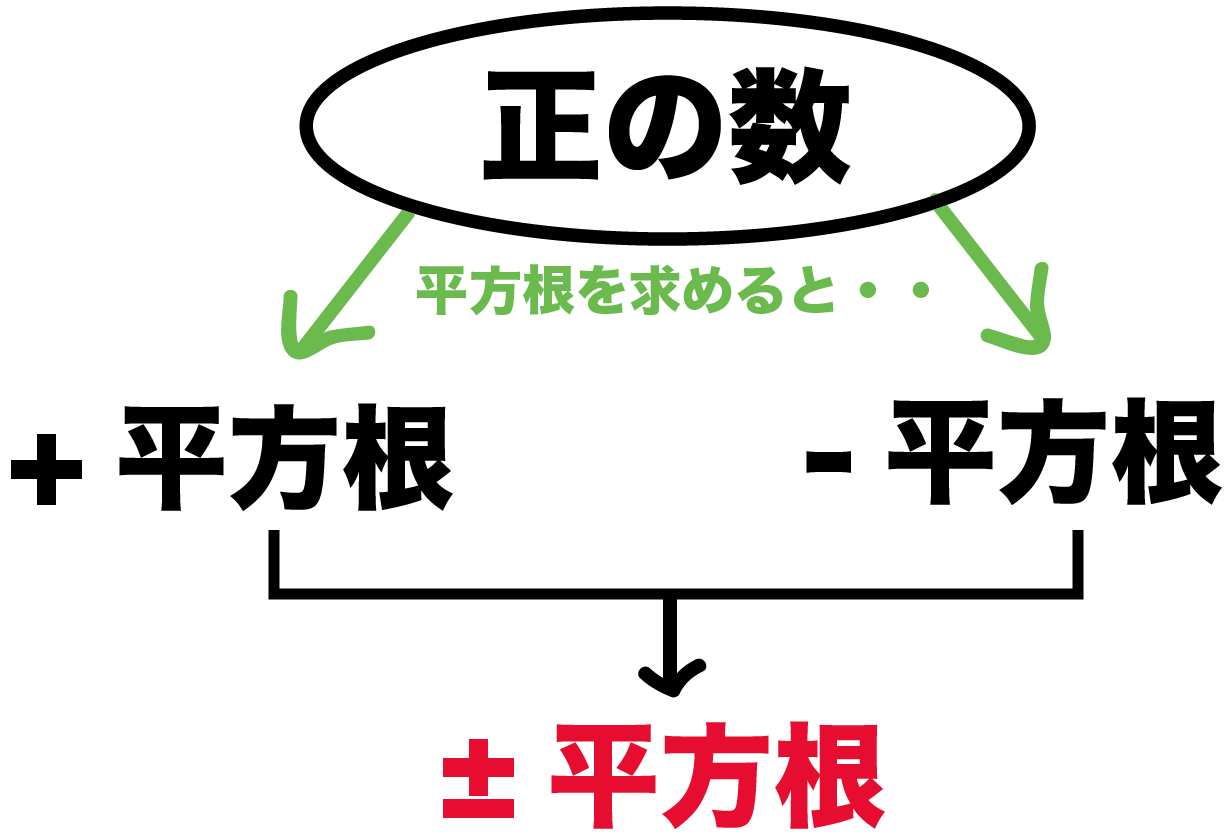



中学数学 3分でわかる 平方根の性質 Qikeru 学びを楽しくわかりやすく
平方根計算法 実行結果 正整数 12の平方根の整数部 = 3 正整数 1234の平方根の整数部 = 35 正整数 の平方根の整数部 = 351 正整数 の平方根の整数部 = 3513 ok 改良 1234の平方根を求める。 1234を2桁ずつに分ける。 ①12の平方根を求める。 0 < 12 135 < 12 < 1357如何手算平方根 有很多方法可以用手就算出平方根。有的别的方法只能得到估计值,这里的方法则可以用简单操作一位一位算出平方根的值。 写出要计算平方根的数字。从小数点开始,将数位分成一对一对的:79,5,7,1477变成"7 95 78 91 47 70"。 我们的例子中,要计算的平方根動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




13 Sqrt 14 Sqrt Sqrtpractice1 C 1 2




これで完璧 平方根の基礎 中3数学 中学生の勉強法




ネッチューくん 1対1ネッツ 今日の一問 0の平方根は ヒント 平方根とはその数に対して 平方すると元の値に等しくなる数のことだよ 数学 一問一答 今日の一問




Vba 数値の絶対値を返す Abs関数 平方根を返す Sqr関数




平方根はなぜプラスとマイナス両方あるの ルートの基本を確認 あんず学習塾のメモ 図表置き場




高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月




Tossランド 平方根 の暗記プリント Dl可




この問題の解き方を教えてください 高校1年の平方根の問題です この問 Okwave
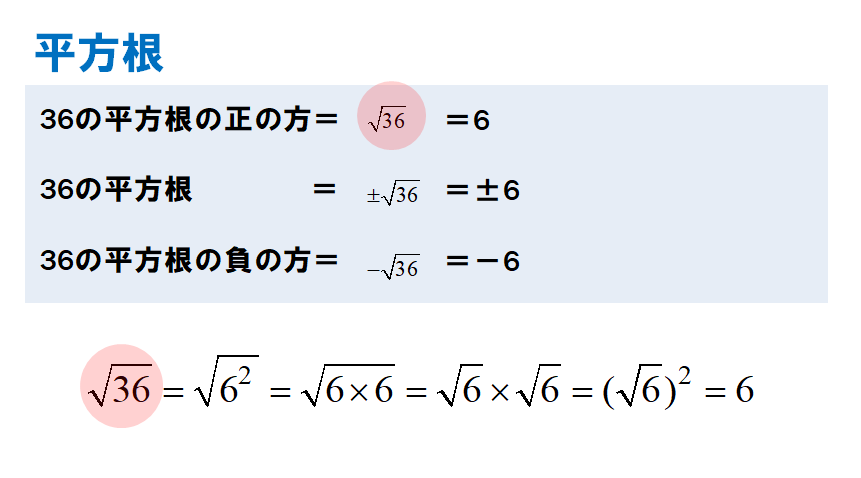



中3数学 平方根の性質の定期テスト対策問題 Examee




ルート64 8ではない のはなぜか 中学数学 定期テスト対策 ベネッセ教育情報サイト



平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師




平方根 加減法 無料で使える中学学習プリント



Www Mext Go Jp Component A Menu Education Detail Icsfiles Afieldfile 0427 Mxt Kouhou02 112 Pdf




平方根 とは 根号の意味や性質 値の求め方について 数学fun




平方根 数学の要点まとめ 練習問題一覧



9の平方根は 3なのに9のルートは3なのはなんででしたっけ ド忘 Yahoo 知恵袋




数学 中3 16 平方根 Youtube




中3数学 平方根 ルートの値を語呂合わせ 覚え方まとめ 数スタ



1




2の平方根 Wikipedia
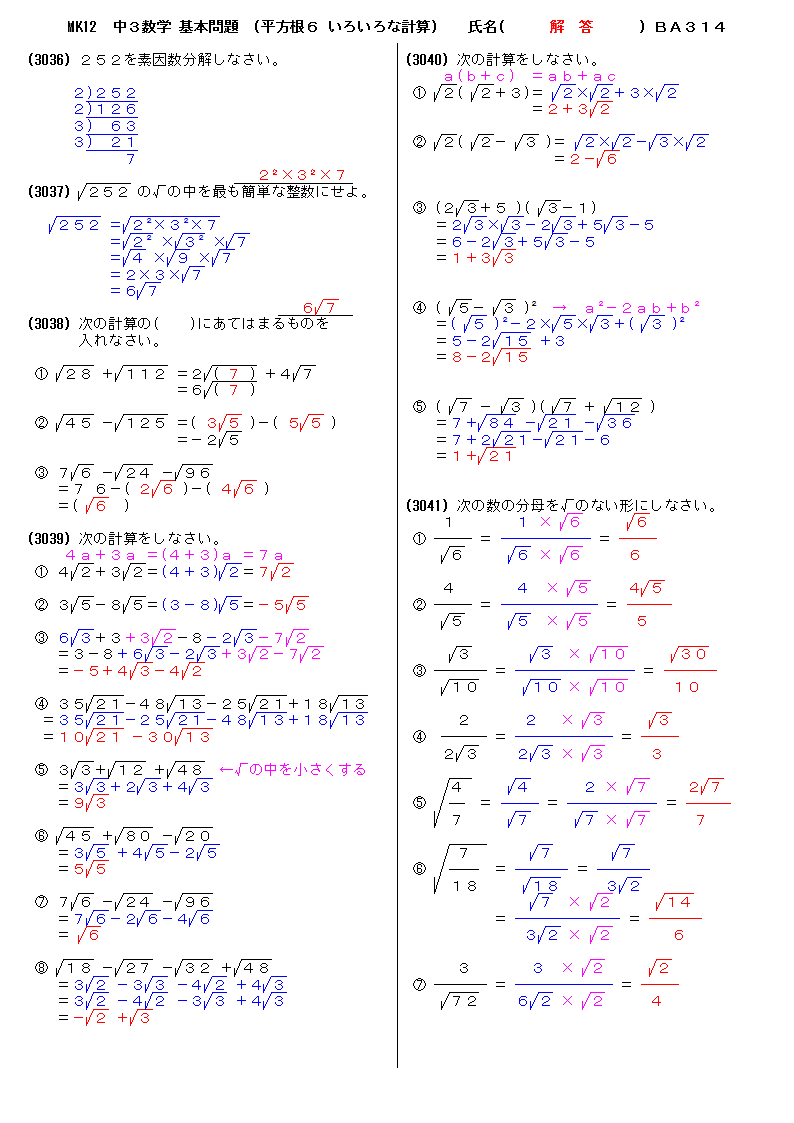



無料 中3数学 基本問題 解答プリント 314 平方根6 いろいろな計算
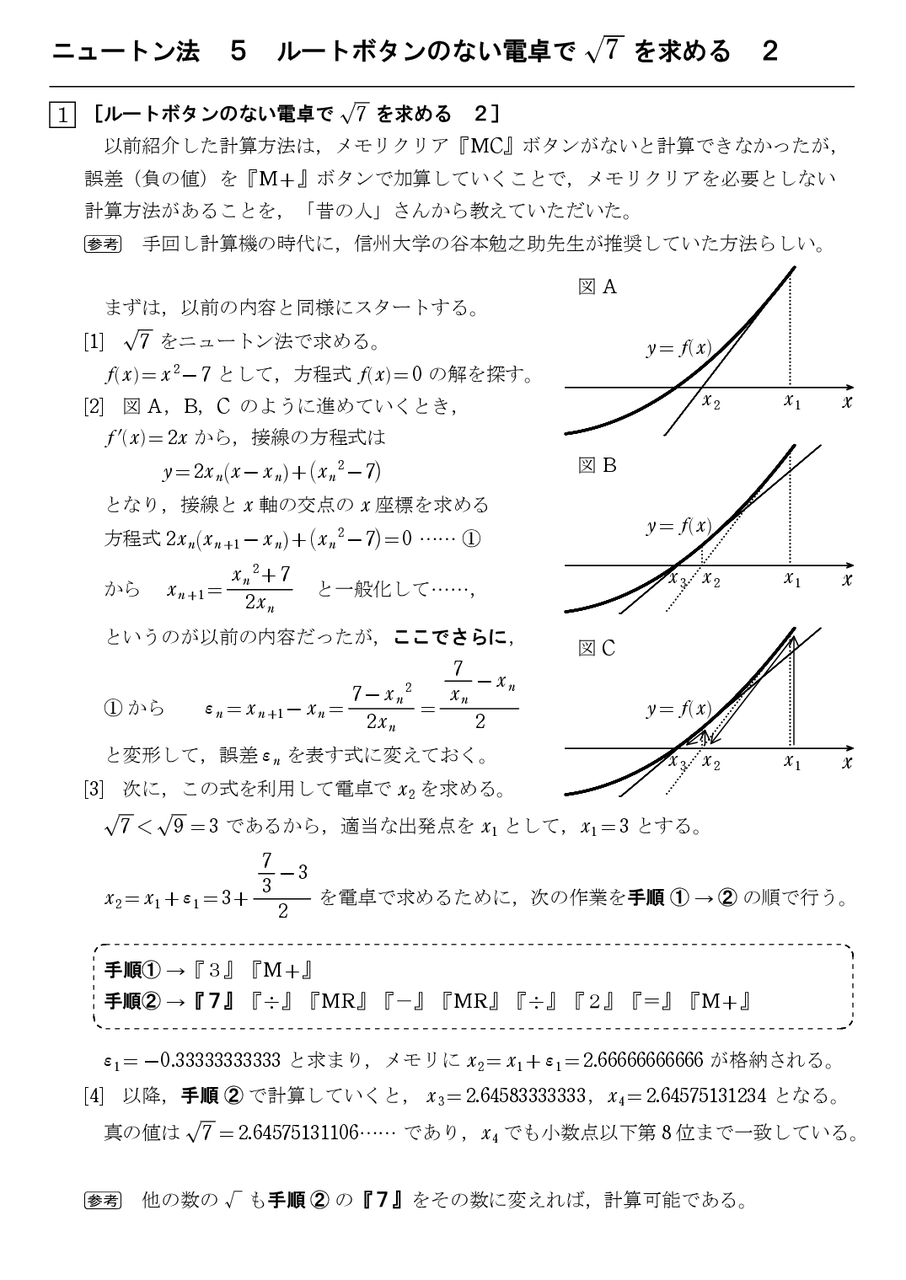



ニュートン法 5 ルートボタンのない電卓で平方根を求める方法 2 怜悧玲瓏 高校数学を天空から俯瞰する




計算機プログラムの構造と解釈 第二版




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




中学3年生 数学 平方根 問題プリント 無料ダウンロード 印刷 このページの答えのプリント 全部




ルート2ルート3ルート5ルート7のゴロ合わせ 素数の平方根の筆算の仕方 アタリマエ




1 196q Descubre Como Resolverlo En Qanda




これで完璧 平方根の基礎 中3数学 中学生の勉強法




勝手に北辰テスト対策 数学 平方根 蒼進塾 そうしんじゅく さいたま市 真剣に努力する姿勢を育む



Q Tbn And9gcqfjlikiomoi2cl59zvfrrailtnnzrsyfl7ksxm8vu0 66opurc Usqp Cau
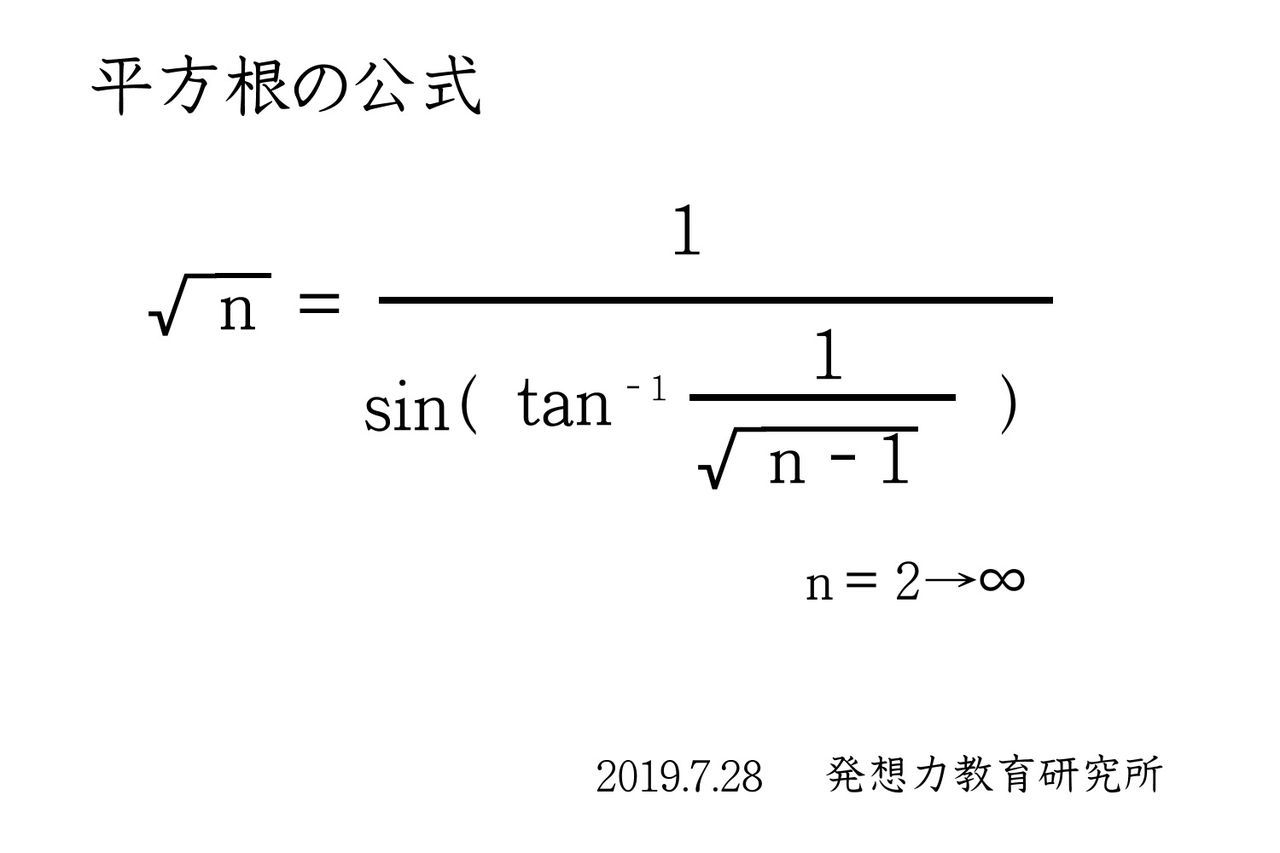



本末転倒の整数論 新発見 平方根の公式 ピタゴラスの誤解が生んだpの迷宮を断つ 発想力教育研究所 素数誕生のメカニズム



Happylilac Net Pdf Jhs Math3 02 01ans Pdf



中学3年生の数学の問題です 49分の36と64分の49の平 Yahoo 知恵袋



平方根 正誤問題 清水塾




中3 平方根 特別編 正誤問題 中学数学の勉強に




中学数学 3分でわかる 平方根の性質 Qikeru 学びを楽しくわかりやすく




中3 7 1 平方根の意味と根号 Youtube




中学数学 3分でわかる 平方根の性質 Qikeru 学びを楽しくわかりやすく



Kumanichi Com Assets Image Examination 18 Sugaku 25 Pdf



1



2乗 平方根




高校 数学 複素数7 負の数の平方根 13分 Youtube




大きな数の平方根 問題 Youtube




平方根はなぜプラスとマイナス両方あるの ルートの基本を確認 あんず学習塾のメモ 図表置き場




中3自習 平方根7 加減1 中学数学の勉強に




平方根とは ルートとは 計算方法と求め方 語呂合わせと覚え方 Rikeinvest
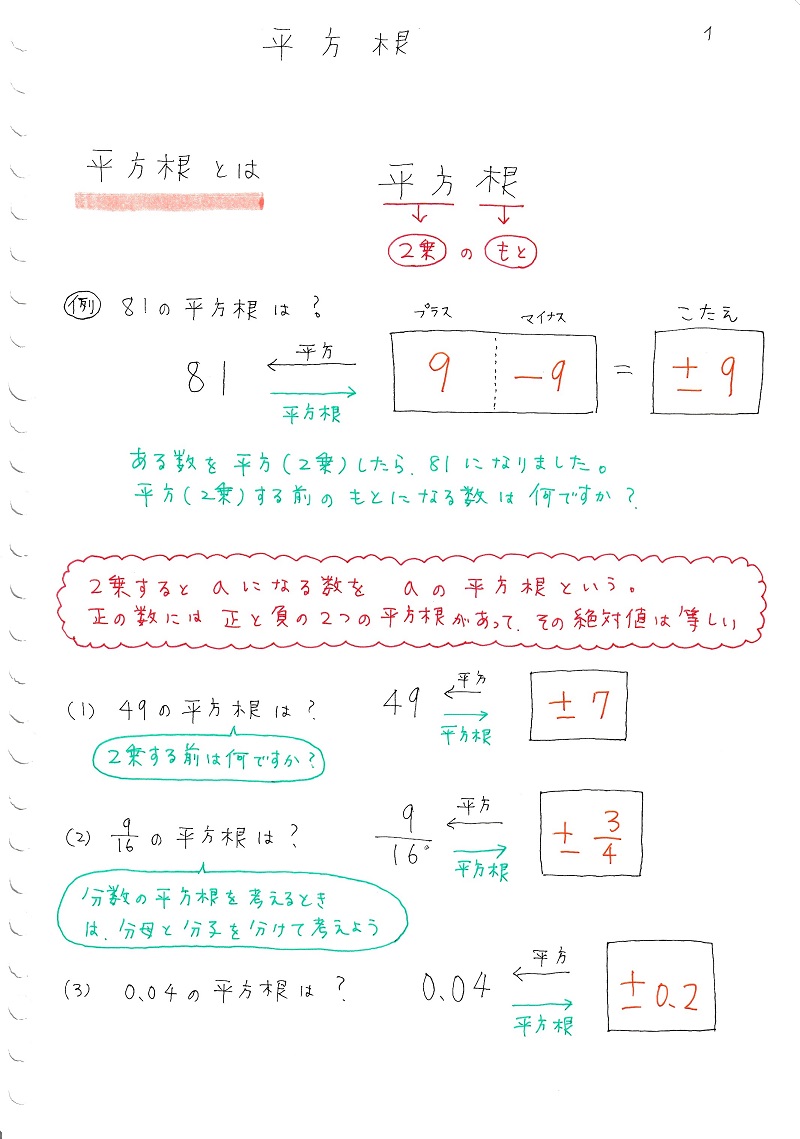



中学数学 平方根 ママ塾ノート
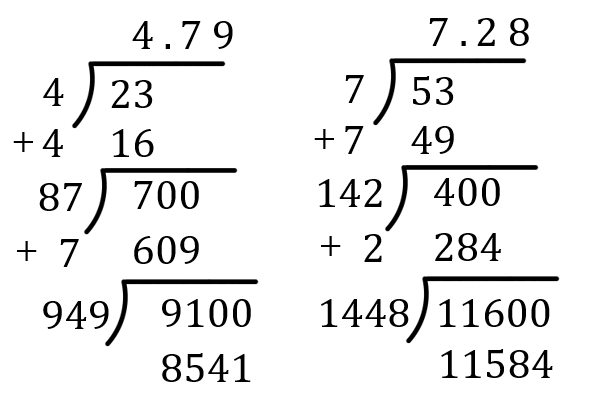



ルート2ルート3ルート5ルート7のゴロ合わせ 素数の平方根の筆算の仕方 アタリマエ




平方根 ルートを整数に直す チーム エン




2 Sqrt016 Descubre Como Resolverlo En Qanda




平方根と実数 中学生の数学 スタンダード 7 森川 幾太郎 本 通販 Amazon




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ



数学 根号を含む計算 平方根など 数学




平方根を簡単にする 3つの方法 Wikihow
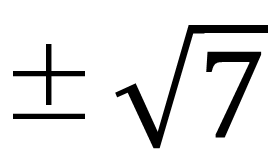



中3数学 平方根 ルート 根号 のかけ算はこれで完璧 たけのこ塾 勉強が苦手な中学生のやる気をのばす



Http Www Edu City Yokohama Lg Jp School Jhs Kohnandai1 Index Cfm 1 2445 C Html 2445 0721 1142 Pdf




Amazon 49の平方根 7歳の誕生日 7歳のプレゼント 長袖tシャツ Tシャツ カットソー 通販




あってますか 多分間違い沢山あると思うので教えてください Clear




勝手に北辰テスト対策 数学 平方根 蒼進塾 そうしんじゅく さいたま市 真剣に努力する姿勢を育む



1
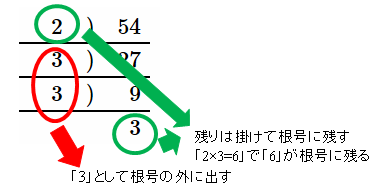



素因数分解 根号の外し方 2 ネット塾




無料 中3数学 基本解説 解答プリント 309 平方根1 意味




中学の数学 平方根 を理解して受験を乗り切ろう 札幌市 学習塾 受験 チーム個別指導塾 大成会




7も実数 中3の平方根 立ち読み計算ドリル ききょうけん キッズの教養を考える研究室



数学3年 平方根 平方根 根号の計算 平方根 平方根 問題1 正解1 解説1 問題2 正解2 解説2 問題3 正解3 解説3 平方根 大小比較 問題4 正解4 解説4 問題5 正解5 解説5 平方根




中3 7 2 平方根の大小 Youtube
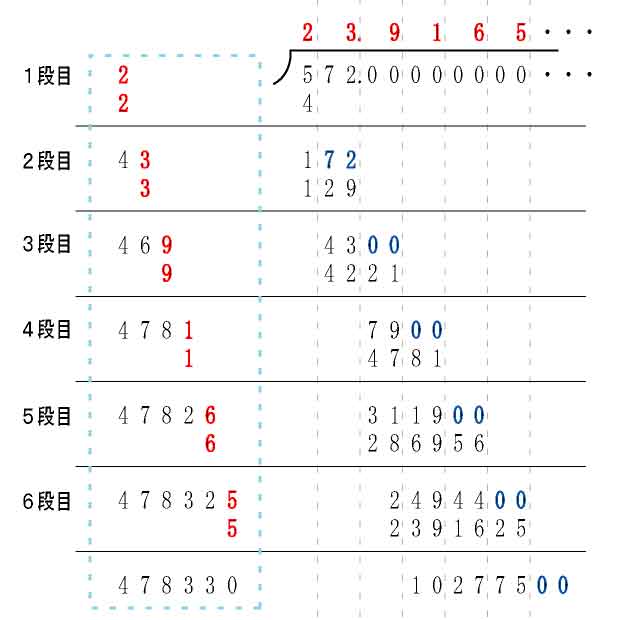



開平方 平方根の求め方 時じくの香の木の実




この問題の違いを教えてください つけるのと付けないのがありますよね Clear




平方根とは サイエンスの人気 最新記事を集めました はてな




日本ケイデンス デザイン システムズ The Sound Of Cadence Online




簡単にわかる 平方根 苦手な数学を簡単に
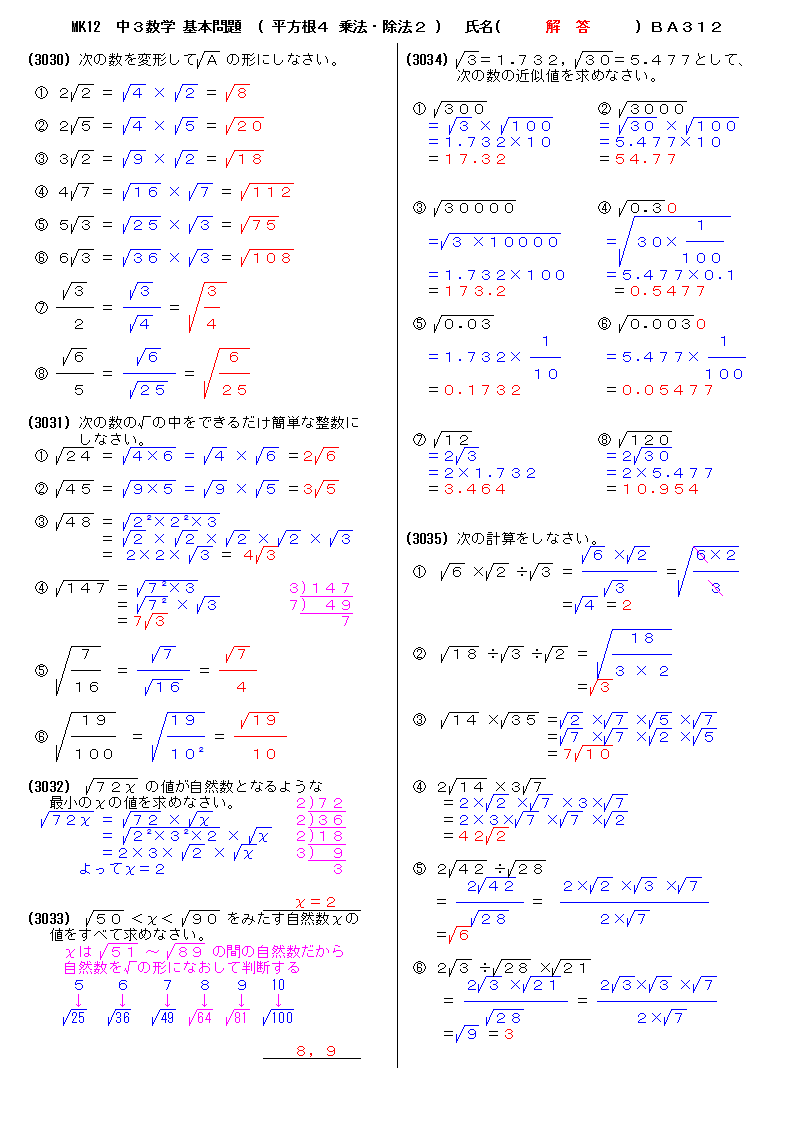



無料 中3数学 基本問題 解答プリント 312 平方根4 乗法 除法2




実数は二乗して負にならないということに質問です Clear




平方根の考えを使った解き方 教遊者




中3 中3 2章 平方根 1節 平方根 中学生 数学のノート Clear




中学数学 平方根のひみつ 都立高校入試で成功する方法




数学力向上委員会 中3 初めての平方根 やはり俺の考察ブログはまちがっている アニメ 数学




平方根の問題の解き方 6パターン 数学fun




この問題の解き方を教えてください 高校1年の平方根の問題です この問 Okwave




中学数学 平方根の利用 ママ塾ノート



3 27第2章平方根 根号を使わずに表す 中学生




8 2 平方根の性質と計算 イ弋マ本ゼミナール




第2講 根号を含む式の計算 1章 2節実数 問題集 高校数学



Www Kyoiku Shuppan Co Jp Ml Jh Files 3nen 2shou Mondai Pdf




Iの平方根 結城浩ミニ文庫 結城浩




中3数学 8 3 平方根 Youtube



Www Shinko Keirin Co Jp Keirinkan Chu Math Support Jiko Test21 Pdf Jh3 2syou Pdf
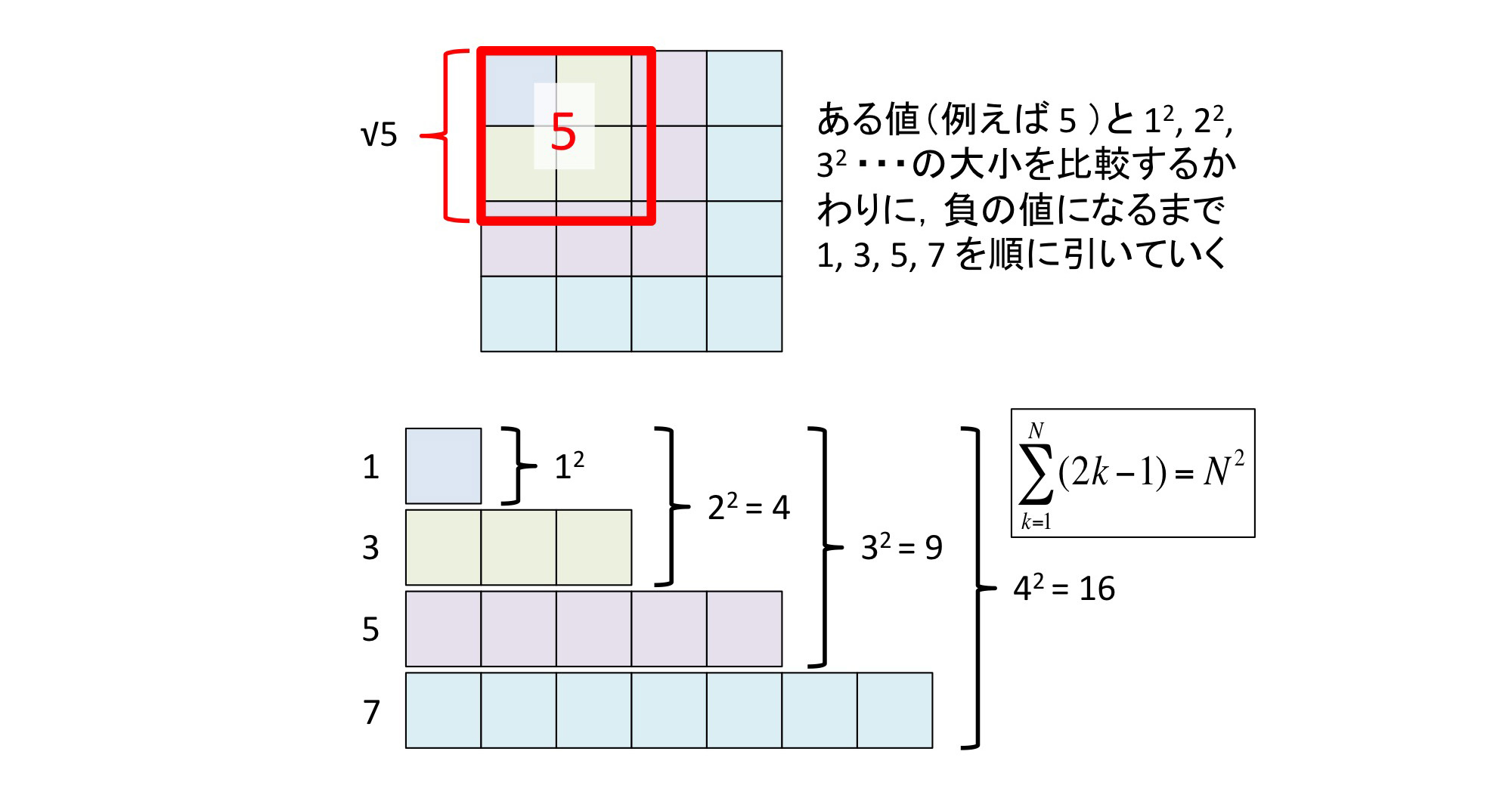



機械式計算機による平方根の計算




4の平方根やルートは 9 16 25 36 49の平方根とルートは 平方根とルートの違い 意味 や計算方法を解説 プラスマイナス More E Life




中学数学 平方根 のコツ 平方根とは 平方根の大小



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス



Www Kyoiku Shuppan Co Jp R3chuu Sugaku Files Dl11 Sugaku Pdf



0 件のコメント:
コメントを投稿